Boundedness for (min,plus)-automata
We prove that the boundedness problem for (min,plus)-automata is decidable. One of the main application of this result is that the star-heigh problem of regular expressions reduces to (a slight extension of) it. The main point is to present a very useful tool in action: Simon's factorisation theorem. This proof scheme has been used in many, many papers recently.
We consider (min,plus)-automata, meaning that an automaton $\A$ computes a function
\[\A : A^* \to \Ninfty\]where $\Ninfty = \N \cup \{\infty\}$, by assigning to a word $w$ the minimum value of a run, where the value of a run is computed by summing the weights along the run.
The boundedness problem asks whether the function $\A$ is bounded, meaning
\[\exists N \in \N,\ \forall w \in A^*,\ \A(w) \le N\]In this note, we will construct an algebraic structure from an automaton generalising the transition monoid for non-deterministic automata. This algebraic structure is a stabilisation monoid. The answer to the boundedness problem can be found by inspecting the stabilisation monoid: the function $\A$ is bounded if and only if the stabilisation monoid induced by $\A$ does not contain an unbounded witness. The correctness proof of this characterisation relies on a generic tool for stabilisation monoids called Simon’s factorisation theorem.
Extending the transition monoid
Let $\A$ be a (min,plus)-automaton. The transition for letter $a$ is given by
\[\Delta(a) \in \Ninfty^{Q \times Q}\]which reads “the cost of going from $p$ to $q$ reading $a$ is $\Delta(a)(p,q)$”. Algebraically, we consider the semiring $(\Ninfty,\min,+)$, inducing similar operations on matrices. The function $\A : A^* \to \Ninfty$ is defined by $\A(w) = I \cdot \Delta(w) \cdot F$ where $I,F \in \Ninfty^Q$ are the initial and final vectors and $\Delta$ is extended to a morphism $A^* \to \Ninfty^{Q \times Q}$.
We also write $\A(w)(s,t)$ for the cost of the minimal run from $s$ to $t$ over the word $w$.
The special case of non-deterministic automata
Let us consider a special case: $\Delta(a) \in \{0,\infty\}^{Q \times Q}$ and $I,F \in \{0,\infty\}^Q$. Then $\A(w) \in \{0,\infty\}$, and $\A$ is essentially a non-deterministic automaton, where $\Delta(a)(p,q) = 0$ means that there exists a transition from $p$ to $q$, and $\A(w) = 0$ if $w$ is accepted. Indeed in algebraic terms the semiring $(\{0,\infty\}, \min, +)$ is isomorphic to the usual boolean semiring $(\{0,1\},\vee,\wedge)$ (where $0$ is mapped to $1$ and $\infty$ to $0$). In this special case, the boundedness problem reduces to the universality problem (note that this implies PSPACE-hardness of the boundedness problem).
We show how to solve the universality problem by computing the transition monoid. The transition monoid $\M_\A$ of a non-deterministic automaton $\A$ is the monoid generated by the matrices $\Delta(a)$ for $a \in A$. In other words, we start from $\{\Delta(a) : a \in A\}$ and close under matrix product. For the sake of explanation let us see $\Delta(a)$ as a matrix in the boolean semiring $(\{0,\infty\}, \min, +)$. Since $\{0,\infty\}^{Q \times Q}$ is finite, the transition monoid $\M_\A$ is finite and can be effectively computed using a simple saturation algorithm.
One can verify that $\A$ is universal if and only if $\M_\A$ does not contain a matrix $M$ such that $I \cdot M \cdot F = \infty$. Indeed, the morphism $\Delta : A^* \to \M_\A$ maps words to matrices in $\M_\A$ and a word $w$ is rejected if $I \cdot \Delta(w) \cdot F = \infty$.
Projecting on a finite semiring
A crucial property for non-deterministic automata is that $\{0,\infty\}^{Q \times Q}$ is finite, implying that the transition monoid is finite, therefore computable. This does not hold anymore for (min,plus)-automata, ie in the semiring $\Ninfty^{Q \times Q}$.
The good news is that for answering the boundedness problem it is enough to project $\Ninfty$ into a finite semiring. The semiring we are looking at contains three elements: $0,1$ and $\infty$. The intuitive meaning is in terms of costs: $0$ is free, $1$ is a small cost, and $\infty$ a large cost. We let $\pi$ denote the projection from $\Ninfty$ to $\{0,1,\infty\}$, which simply sends $0$ to $0$, any finite value to $1$ and $\infty$ to $\infty$.
The two operations are $\min$ and $+$, with the expected semantics. \(\begin{array}{c||c|c|c} \quad \min \quad & \quad 0 \quad & \quad 1 \quad & \quad \infty \quad\\ \hline 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ \infty & 0 & 1 & \infty \\ \end{array} \hspace{1cm} \begin{array}{c||c|c|c} \quad + \quad & \quad 0 \quad & \quad 1 \quad & \quad \infty \quad\\ \hline 0 & 0 & 1 & \infty \\ 1 & 1 & \textbf{1} & \infty \\ \infty & \infty & \infty & \infty \\ \end{array}\)
Using these two operations we can multiply matrices in $\{0,1,\infty\}^{Q \times Q}$.
Stabilisation
We bring a new operator called stabilisation. Consider the following weighted automaton (can it be simpler?).

We have $\A(a) = 1$. The function $\A$ is unbounded, because $\A(a^n) = n$, diverges for $n \to \infty$. Hence we need an operator to capture the behaviour of a repeated sequence; the stabilisation operator will do just that!
Define
\[0^\sharp = 0 \quad 1^\sharp = \infty \quad \infty^\sharp = \infty\]At an intuitive level: $\sharp$ corresponds to iterating. Repeating a large number of times an operation with cost $0$ yields an operation with cost $0$. However, if each operation costs $1$, the whole operation becomes very costly.
A matrix $M$ is idempotent if $M^2 = M$. The stabilisation operator over matrices is defined for idempotent matrices by
\[M^\sharp(s,t) = \min \left\{ M(s,p) + M(p,p)^\sharp + M(p,t) : p \in Q \right\}\]Intuitively: how much does it cost to go from $s$ to $t$ by repeating the action $M$ a large number of times? The path achieving the minimum goes from $s$ to some $p$, follows a loop around $p$, and then from $p$ to $t$, with the whole operation of cost $M(s,p) + M(p,p)^\sharp + M(p,t)$.
We now have a unary operation on (idempotent) matrices. What we have done is defining a stabilisation monoid, which is given by a set (here matrices over $\{0,1,\infty\}$), a binary operation (multiplication of matrices) and a unary operation called stabilisation.
The stabilisation monoid of a (min,plus)-automaton
Given a (min,plus)-automaton $\A$, we define its stabilisation monoid $\M_\A$ to be the stabilisation monoid generated by the matrices $\pi(\Delta(a))$ for $a \in A$. For convenience we let $\mathbf{a}$ denote $\pi(\Delta(a))$. In other words, we start from $\{\mathbf{a} : a \in A\}$ and close under matrix product and stabilisation. Since the underlying semiring is finite, the stabilisation monoid is finite and can be effectively computed using a simple saturation algorithm.
We say that a matrix $M$ is an unbounded witness if $I \cdot M \cdot F = \infty$.
Theorem: Let $\A$ be a (min,plus)-automaton. $\A$ is bounded if and only if $\M_\A$ does not contain any unbounded witness
This yields an algorithm for deciding boundedness. A naive implementation is in EXPTIME; a further analysis of the stabilisation monoid gives a PSPACE algorithm.
One direction is easy: let $M \in \M_\A$ be an unbounded witness. One can associate with $M$ a $\sharp$-expression explaining how $M$ was computed in $\M_\A$: for instance, $((a^\sharp) b)^\sharp$ represents the computation:
- first apply the stabilisation operator to $\mathbf{a}$
- then multiply the result with $\mathbf{b}$
- finally apply the stabilisation operator to the result
Following the inductive construction of the $\sharp$-expression, one can construct a sequence of words $(w_n)_{n \in \N}$ (essentially replacing $\sharp$ by $n$) such that
\[\lim_n\ \A(w_n)(p,q) = \infty \text{ if and only if } M(p,q) = \omega\]Hence the fact that $M$ is an unbounded witness implies that $\lim_n \A(w_n) = \infty$.
In the remainder of this post we prove the converse more challenging implication, called completeness.
Simon’s factorisation theorem
Imagine that we have some (min,plus)-automaton $\A$ and we are looking at $\A(w)$ for some word $w$ (which we can think of as very long), for instance
\[(ab)^{300000}\]As an approximation let us think of this word as $(ab)^n$ for a very large $n$. We want to know whether $\A((ab)^n)$ is large, or in other words whether it diverges to infinity when $n \to \infty$: this is equivalent to asking whether $I \cdot (\mathbf{a} \cdot \mathbf{b})^\sharp \cdot F = \omega$.
The word $(ab)^{300000}$ had an obvious factorisation into $(ab)^n$ for a large $n$. Simon’s factorisation theorem says that any word can be factorised in a similar way. Let us formalise this notion of factorisation. Let $\M$ be a stabilisation monoid and a morphism $\phi : A^* \to \M$, the factorisation of $\phi(w)$ is a tree such that
- each node is labeled by a pair $(M,u)$ where $M \in \M$ and $u \in A^*$
- the leaves are labeled by $(\phi(a),a)$ for $a \in A$
- reading the second component of the leaves from left to right yields the word $w$
- the internal nodes are of two types: product nodes and stabilisation nodes
- a product node has two children, let $(M_1,w_1)$ and $(M_2,w_2)$ be their labels, then the label of the node is $(M_1 \cdot M_2, w_1 w_2)$
- a stabilisation node has $k \ge 3$ children, let $(M,w_i)$ be their labels, then $M$ is an idempotent of $\M$ (meaning $M^2 = M$) and the label of the node is $(M^\sharp, w_1 \cdots w_k)$
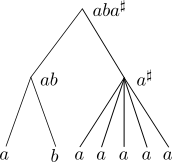
Theorem: Let $\M$ be a stabilisation monoid and a morphism $\phi : A^* \to \M$. There exists a constant $K$ such that for all words $w \in A^*$, there exists a factorisation of $\phi(w)$ of depth $K$
The theorem says that no matter of long, complicated and messy a word is, it can be factorised through $\phi$ by a tree of constant depth. Here constant means that the value depends on $\M$ but not on the word. The optimal $K$ is $3|\M|$.
Finishing the proof
Let us assume that there are no unbounded witness and prove that $\A$ is bounded. Consider a word $w$. Thanks to Simon’s factorisation theorem applied to the morphism $\phi : A^* \to \M_\A$ defined by
\[\phi(a) = \mathbf{a},\]there exists a factorisation of $\phi(w)$ of depth $K$. We will reason on this tree.
We let $W$ denote the maximal weight appearing in the (min,plus)-automaton $\A$.
Lemma: For all nodes labeled $(M,u)$ at distance $d$ from the leaves, for all states $s,t$ we have \(\begin{array}{ccc} M(s,t) = 0 & \implies & \A(u)(s,t) = 0 \\ M(s,t) = 1 & \implies & \A(u)(s,t) \le 2^d \cdot W \end{array}\)
We prove the lemma by induction from the leaves to the root.
- If the node is a leaf this is by definition of $\phi(a)$ and $W$.
- If the node is a product node labeled $(M_1 M_2,w_1 w_2)$. The first item is easy to prove, let us focus on the second. Assume $(M_1 M_2)(s,t) = 1$, this implies that there exists $p$ such that $M_1(s,p) = 1$ and $M_2(p,t) = 1$. It follows by induction hypothesis that $\A(u)(s,t) \le \A(u_1)(s,p) + \A(u_2)(p,t) \le 2 \cdot 2^{d-1} \cdot W$.
- If the node is a stabilisation node labeled $(M^\sharp,w_1 \ldots w_k)$. Again we only prove the second item, the first one is easy. Assume $(M^\sharp)(s,t) = 1$, this implies that there exists $p$ such that \(M(s,p) + M^\sharp(p,p) + M(p,t) = 1\) so $M(s,p) = M(p,t) = 1$ and $M(p,p) = 0$. It follows by induction hypothesis that
We can now finish the proof of completeness. Since $\M_\A$ does not contain any unbounded witness, the previous lemma implies that $\A(w)$ is bounded by $2^K W$ where $K$ is the constant inherited from Simon’s factorisation theorem.