Generalized reachability games
This post is about generalized reachability games. The main purpose is to pose an open problem: what is the complexity of solving 2-generalized reachability games?
This post is about this paper. This is the first research paper I have worked on (with Florian Horn). It has some cool results but despite years of efforts we never managed to solve the last question. The goal of this post is to entice the reader to attack it!
We consider two-player games played on graphs. The two players are Eve and Adam. The vertices are either circles, meaning that they are controlled by Eve, or squares, meaning that they are controlled by Adam. If you are not familiar with this framework please check out the paper.
A very classical objective is Reachability: given a set of vertices $F$, Eve wins if she ensures that some vertex from $F$ is reached at least once during the play.
This paper introduces Generalized reachability objectives: given a family of sets $F_1,\ldots,F_k$, Eve wins if she ensures that for each $i \in [1,k]$, some vertex from $F_i$ is reached at least once during the play. It is very important to note here that the order under which the sets are visited is not specified.
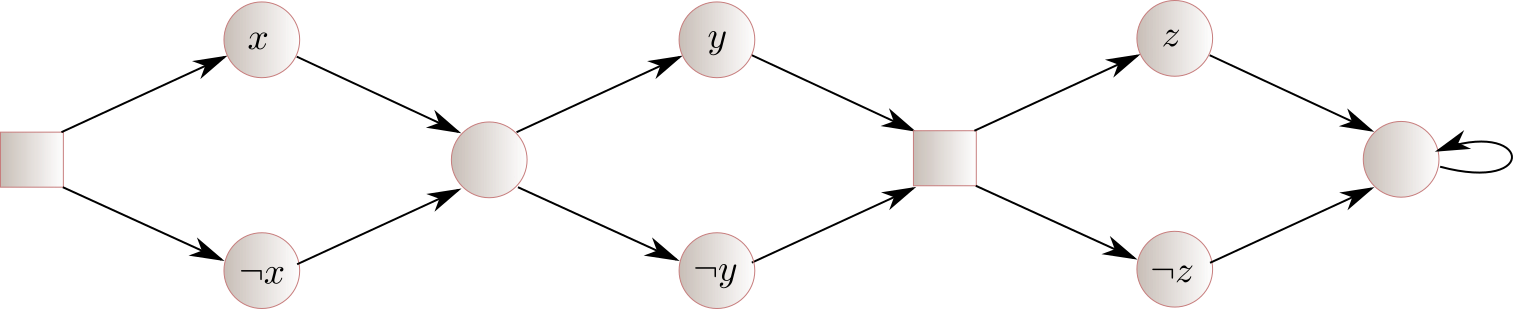
As a first example and to help intuition, we show that generalized reachability games include the QBF problem. Consider the QBF formula
\[\forall x\ \exists y\ \forall z\ (x \vee \neg y) \wedge (\neg y \vee z)\ .\]The generalized reachability game is shown below. Eve takes care of existential quantification, and Adam of universal quantification. The clauses correspond to the sets $F_i$: here we have $F_1 = \{x, \neg y\}, F_2 = \{\neg y,z\}$.
We are interested in two questions:
- complexity of the following decision problem: given a generalized reachability game, determine whether Eve has a winning strategy
- for different subclasses, how much memory is required for constructing winning strategies for both players
The main restriction we consider is the size of the sets $F_i$ which for QBF corresponds to restricting the size of the clauses.
What is known
Theorem: (Solving games)
- Solving generalized reachability games is PSPACE-complete, even if each set $F_i$ has size $3$
- Solving generalized reachability games for a fixed $k$ is in PTIME
- Solving generalized reachability games when each set $F_i$ is a singleton is in PTIME
The first two items are hardly surprising. The third one is more interesting, a full proof can be found in the paper.
Theorem: (Memory for Eve)
- In general, Eve needs exactly $2^k - 1$ memory states, matching upper and lower bounds
- When each set $F_i$ has size $1$, Eve needs exactly $k$ memory states, matching upper and lower bounds
Theorem: (Memory for Adam)
- In general, Adam needs exactly $\binom{k}{k/2}$ memory states, matching upper and lower bounds
- When each set $F_i$ has size $1$, Adam needs exactly $2$ memory states, matching upper and lower bounds
The first item for Adam is non-trivial, it relies on interesting observations related to the lattice underlying Adam’s canonical memory structure. The number $\binom{k}{k/2}$ is the size of the largest antichain in the lattice of subsets of $[1,k]$ for the inclusion. Shameful advertising: this result was extended for all topologically closed objectives in this paper.
The open question
The case where each set $F_i$ has size $2$ is widely open. It contains 2-QBF, ie the subproblem of QBF where each clause has size at most $2$, which is known to be in PTIME.
We know a few facts about this case
- Eve needs at least $2^{k/2}$ memory states and at most $2^k - 1$
- Solving the one-player variants where either only Eve plays or only Adam plays is in PTIME
- Adam needs at least $4$ memory states
The second item is a not so obvious reduction to 2-SAT. The third item is a funky example proposed by Christof Loeding, see the paper. Strangely enough, $4$ seems to be the best we can do with this idea.
Open question: what is the complexity of solving generalized reachability games where each $F_i$ has size $2$?
The complexity can be anywhere between PTIME and PSPACE.
Conjecture: Adam needs at most $4$ memory states to win in a generalized reachability game where each $F_i$ has size $2$. This number reduces to $2$ if the game is acyclic.
This conjecture would imply a $\text{coNP}^{\text{NP}}$ algorithm: guess a strategy for Adam, compose it with the game, and solve the resulting one-player game.
To avoid Stefan Kiefer’s conundrum I’m not offering 100€ for solving this problem, but instead and if you’re interested I’d definitely offer a PhD / postdoc / visit to LaBRI, Bordeaux! This holds even only for a non-trivial complexity upper or lower bound, even in the acyclic case!