Minimising weighted tree automata and context-free grammars
We discuss an extension of Fliess' theorem for minimising weighted tree automata.
This post is somehow a follow-up of this one, but it can be read independently.
Minimising weighted tree automata
We consider tree formal series (here over the reals), i.e. functions \(f : Tree(A) \to \R\). Here A is a signature, it contains letters with arities, for instance $a(2)$ and $b(0)$.
A context is a tree over the signature $A \cup \{ \square(0) \}$, with the restriction that $\square$ appears exactly once. We write $\Context(A)$ for the set of contexts.
A context $c$ and a tree $t$ yield a tree $c[t]$ simply by substituting in $c$ the leaf $\square$ by the tree $t$.
The Hankel matrix of \(f\) is a bi-infinite matrix \(H_f \in \R^{\Context(A) \times \Tree(A)}\) defined by
\[H_f(u,v) = f( c[t] )\]For recognising formal series we use weighted tree automata, which we do not define here but naturally extend the word case.
The following theorem of Bozapalidis and Louscou-Bozapalidou naturally extends Fliess’ theorem.
Theorem: (Bozapalidis and Louscou-Bozapalidou 1983)
- Any weighted tree automaton recognising $f$ has at least $\rk(H_f)$ many states,
- There exists a weighted tree automaton recognising $f$ with $\rk(H_f)$ many states.
Minimising weighted context-free grammars
A weighted context-free grammar is a context-free grammar (over words) which comes with a weight function on rules. Such a grammar defines a function $f : A^* \to \R$: the value of a derivation is the product of the weights of the rules, and the value of a word is the sum of the value of the runs.
We know that the Hankel matrix for functions $f : A^* \to \R$ can be used to characterise functions recognised by weighted automata. Unsurprisingly, weighted context-free grammars are more powerful, and the Hankel matrix as defined in this case does not contain enough information (it may have infinite rank although the function is defined by a weighted context-free grammar).
The paper of Bailly, Carreras, Luque, and Quattoni presents a wrong Hankel-like theorem for weighted context-free grammars. We give here a counter-example.
The idea is to consider functions \(f : (A^* \times A^*) \times A^* \to \R\). For a weighted context-free grammar $G$ computing $[G]$, the definition of $f$ is
\[f((x,y), z) = \sum_{A \text{ non-terminal of } G} [G](S \to x A y) \cdot [G](A \to z)\]Intuitively, we restrict the computations of $x z y$ to those having a cut in $z$. In the same way as for tree automata, $(x,y)$ is a sort of context (although only its yield).
The Hankel matrix of such a function \(f\) is a bi-infinite matrix \(H_f \in \R^{(A^* \times A^*) \times A^*}\) defined by
\[H_f((x,y) , z) = f((x,y), z)\]The surprising claim is that this is enough information to recover the whole grammar. It is not, and we give now a counter-example.
More precisely, the wrong claim is that for any \(f : (A^* \times A^*) \times A^* \to \R\), one can construct a weighted context-free grammar computing $f$ with the number of non-terminals being the rank of \(H_f\).
We start from the function \(g : Tree(A) \to \R\) assigning $1$ to the following two trees, and $0$ to any other tree.
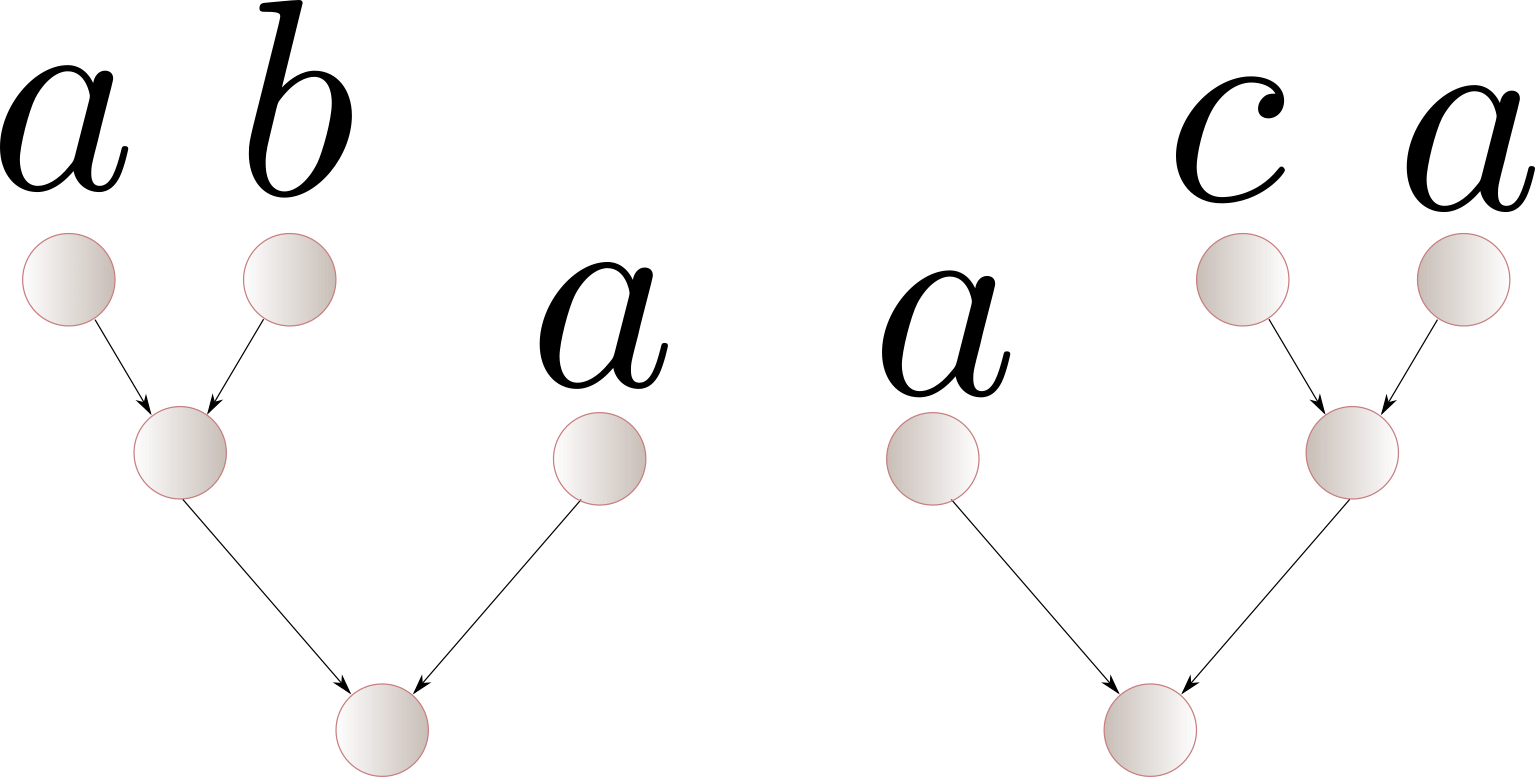
The tree Hankel matrix has rank $6$. One can indeed construct a weighted tree automaton with $6$ states recognising $g$. We present it as a weighted context-free grammar using $6$ non-terminals.
\[\begin{array}{ccc} S & \to & [ab] [a] \\ S & \to & [a] [ca] \\ [ab] & \to & [a] [b] \\ [ca] & \to & [c] [a] \\ [a] & \to & a \\ [b] & \to & b \\ [c] & \to & c \end{array}\]If now we consider the function \(f : (A^* \times A^*) \times A^* \to \R\) defined by
\[f( (x,y), z) = \sum_{t \text{ tree yielding } (x,y),z} g(t)\]When looking at the Hankel matrix for the function $f$, it is almost exactly the same as the function $g$. The only difference is for the row $(a,a)$, which corresponds to the following two contexts.

Because of this, the Hankel matrix for $f$ has size $5$ (instead of $6$). However, there exists no weighted context-free grammar with $5$ non-terminals computing $f$.