Parity games, the quasipolynomial era
This post is an overview on my recent research related to the quasipolynomial time algorithms for parity games. It can serve as a roadmap for various posts on this blog.
Another piece of material for these results is the slides for my invited talk at GanDALF.
The key underlying combinatorial notion is that of universal trees. All quasipolynomial algorithms (and some others) belong to one of three families: separating automata, value iteration, and fixed point. Each algorithm in these families corresponds to the choice of a universal tree, which dictates its complexity.
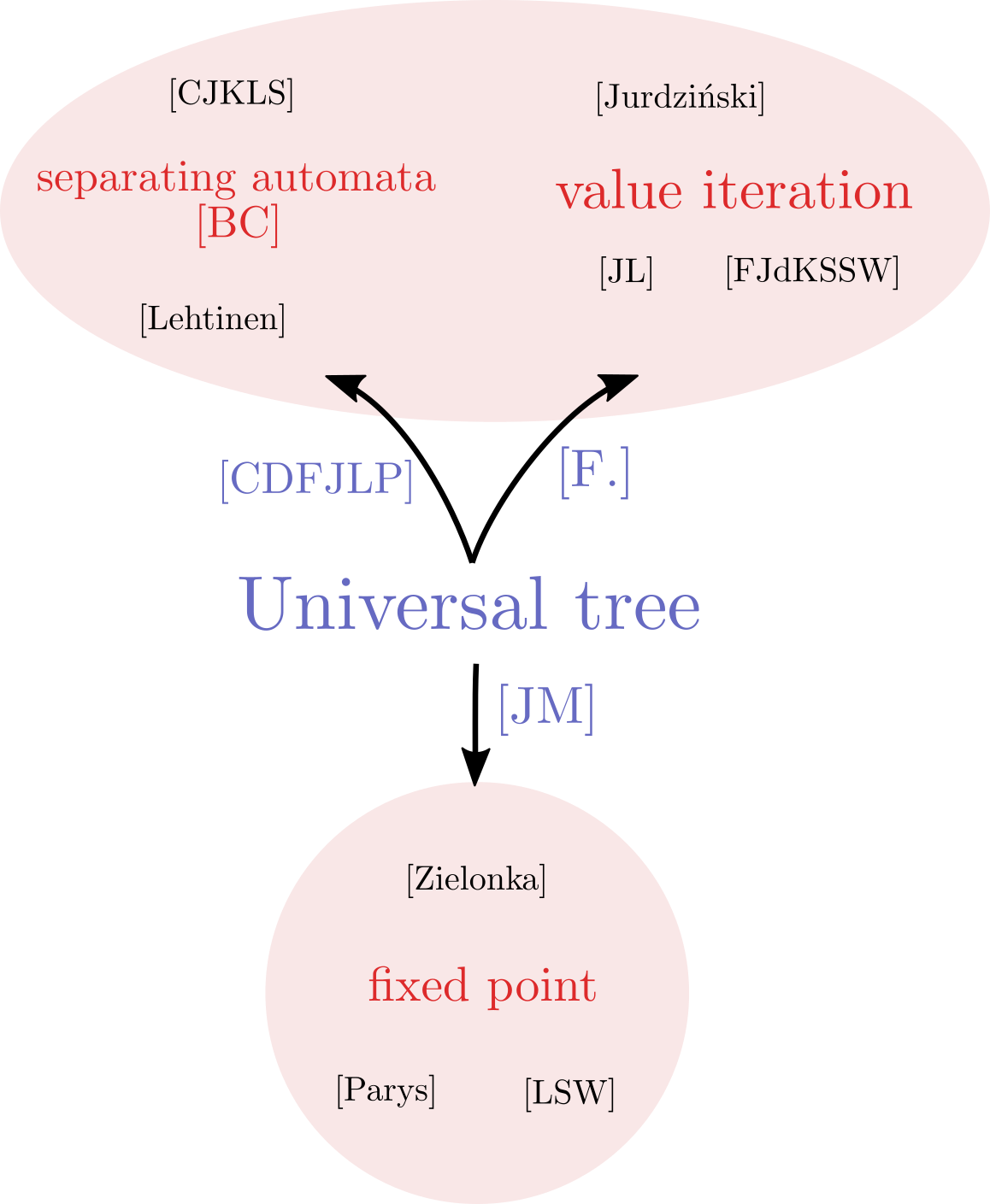
Everything there is to know about universal trees can be found in this post.
The first family of algorithms, the closest to universal trees, is value iteration algorithms. It is presented in this post, and relies on the fundamental theorem for parity games presented in this post. The paper [F.] presents the generic value iteration algorithm using universal trees.
The second family of algorithms is described using separating automata. It is presented in this post. There are two aspects to be discussed. First, the separation question can come in two flavours, strong and weak, we refer to this post. Second, the definition of separating automata requires deterministic automata, which does not cover Lehtinen’s approach; hence a more suitable notion, extending separating automata, is good for small games automata. There are no blog posts on them (yet?), so we refer to this paper.
The first equivalence result states that separating automata and universal trees are equivalent. The original proof is this result is in [CDFJLP]. A conceptually simpler proof introduces and uses the notion of universal graphs, discussed in this post. One of the advantage of this new proof is that it applies to any positionally determined objective, as explained in this post.
Since the notion of universal graphs applies to much more objectives (said differently: universal trees are universal graphs for parity objectives), it opens many perspectives, of constructing new efficient algorithms for other games. We discuss algorithms using universal graphs for mean payoff in this post.
Unfortunately there are no blog posts yet on the third family of algorithms.
Other references in the picture
- [CJKLS]
- [BC]
- [Lehtinen]
- [CDFJLP]
- [FJdKSSW]
- [Jurdziński]
- [JL]
- [F]
- [JM] Marcin Jurdziński and Rémi Morvan, ongoing (personal communication)
- [Zielonka]
- [Parys]
- [LSW]
Edits
28/09: Added references, including personal communication with Marcin Jurdziński and Rémi Morvan.